时间序列_金融思维模型之“时间序列”

篇首语：本文由编程笔记#小编为大家整理，主要介绍了金融思维模型之“时间序列”相关的知识，希望对你有一定的参考价值。

在金融领域里，如果说那种数据组织方式是最主要的，那就非“时间序列”莫属啦。从股票的价格，到GDP的数值，再到公司的财务数据，都随着时间的演进而不停的变化。按照时间的先后顺序，将观察变量在不同时点的不同数值组织起来，构成一个序列，就称之为“时间序列”。

在这一篇中，我们就来谈谈“时间序列”，及其常用的分析方法和它们背后蕴含的金融思维。

什么是时间序列

如果我们对某一个或者某一组变量x(t)进行观察测量，在一系列的时刻t1,t2,…,tn，得到变量的观察值x1,x2,…,xn，这组数字就构成了时间序列。

例如，某只股票在2018年1月1日至2018年8月8日的每日收盘价，就构成了一个时间序列。每个季度国家统计局发布的GDP增长数字，也构成了一个时间序列。

时间序列常常具备以下的几个特征：

• 趋势：是时间序列在长时期内呈现出来的持续向上或持续向下的变动。




• 季节变动：是时间序列在一年内重复出现的周期性波动。它是诸如气候条件、生产条件、节假日或人们的风俗习惯等各种因素影响的结果。




• 循环波动：是时间序列呈现出的非固定长度的周期性变动。循环波动的周期可能会持续一段时间，但与趋势不同，它不是朝着单一方向的持续变动，而是涨落相间的交替波动。




• 不规则波动：是时间序列中除去趋势、季节变动和周期波动之后的随机波动。不规则波动通常总是夹杂在时间序列中，致使时间序列产生一种波浪形或震荡式的变动。只含有随机波动的序列也称为平稳序列。

在时间序列的各个特性中，平稳性具有特殊重要的意义。粗略的讲，所谓平稳时间序列是指，该序列的均值没有系统的变化（无趋势）、方差也没有系统的变化（固定波动），且严格消除了周期性变化。我们来看一个例子。

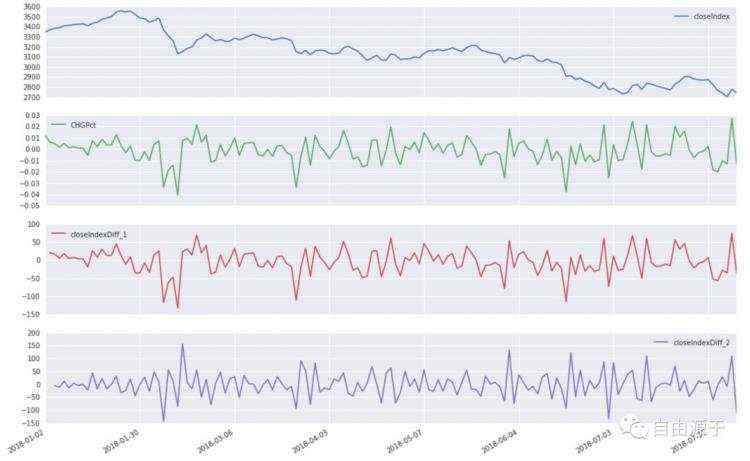
时间序列的样本

上图中的第一张子图为上证综指今年以来的收盘点数，是一个非平稳时间序列；第二张子图是上证综指每天的涨跌幅，平稳性要好了很多；第三张和第四张子图是依次对第二张子图中的时间序列进行差分处理，随着差分的进行，均值和方差基本平稳，因而成为了平稳时间序列。

在数学上，平稳性有两个层级的定义，这里我们用通俗的语言简单加以概括：

• 严平稳：时间序列中任意两个长度相等的子段，其联合分布相同。表达了时间序列的时间平移不变性。




• 弱平稳：时间序列的均值为常数，任意两个长度相同的子段之间的协方差相同。

在金融数据中，通常我们所说的平稳序列，是指弱平稳的序列。如果一个时间序列不是平稳的，通常我们可以通过一次或者多次的差分操作，将它转换成为弱平稳或者近似弱平稳的时间序列。

这里大家对时间序列的平稳性有一个直观的概念就可以了，后面还会用到它。

如何表达时间序列

从信号与系统的角度来看，时间序列可以看作是对信号的定时采用。因而，不同的时间序列可能有不同的采样频率。

采样频率

通常，金融数据的采样频率有如下几种：

• 实时：股票或者期货市场中实时价格数据，也称为Tick数据，这是目前最高频的金融时间序列啦。




• 分钟：交易数据中常见的有1分钟，5分钟，30分钟，60分钟的价格数据，技术分析中很常用。




• 每日：盘后，交易数据会形成当天的收盘价格，根据它可以计算当日的各种技术指标，每股数据等，比如20日均价以及市盈率。




• 每月：经济数据中，国家统计局会发布月度房地产开发投资，进出口数据，发电量，社会消费品零售总额，城镇固定资产投资，规模以上工业增加值等宏观经济数据。




• 每季：上市公司的财务报表需要每季度发布，国家统计局会发布GDP，CPI，PPI等宏观经济数据。基金公司需要发布季报。




• 半年：上市公司需要发布半年度财务报表。基金公司需要发布半年报。




• 年度：上市公司需要发布年度财务报表。基金公司需要发布年度报告。

不同采样频率的时间序列示例

序列插值

在量化分析中，我们主要针对的就是金融时间序列。由于不同时间序列的采样频率不同，通常需要通过序列插值将参与计算的时间序列进行同频化。举个例子，比如我们需要计算股票的每日市盈率。我们知道，财务数据的发布频率是每季，股票收盘价格数据是每日的，这样我们需要先将财务数据从每季扩频插值到每日，然后就可以通过价格除以每股收益来得到当日的市盈率了。

这种财务数据的扩频插值方法，常用的有以下几种，我们以市盈率为例：

• 静态插值：当前的总市值 / 上一年度的公司净利润。在新的年度净利润发布之前，都是用上一年度的。




• TTM插值：当前的总市值 / 最近四个季度的净利润之和。在新的季度净利润发布之后，将其加入计算，而将之前最早的那个季度数据丢弃。




• 动态插值：当前的总市值 / 未来一年的预测净利润。在新的预测发布之前，一直使用当前的预测。

在实际使用中，TTM插值最为常用。它可以调和不同公司选择不同的财务报表发布日期，比如美股允许上市公司自行选择财务年度的截止时间，从而导致同一时间有的公司在发上年年报，而有的公司却在发当年中报。

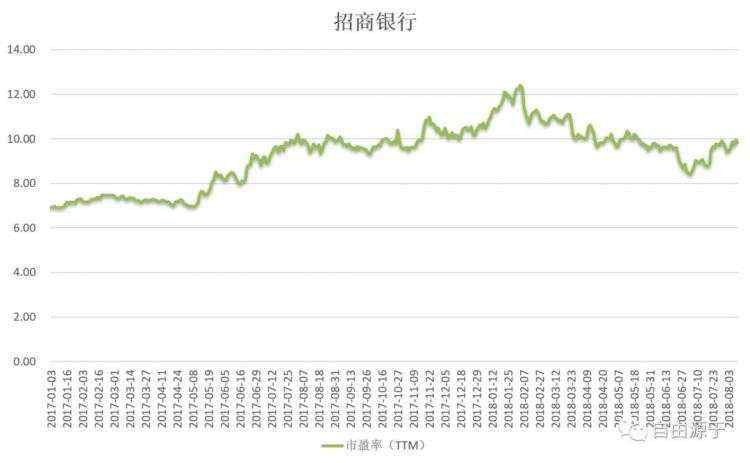
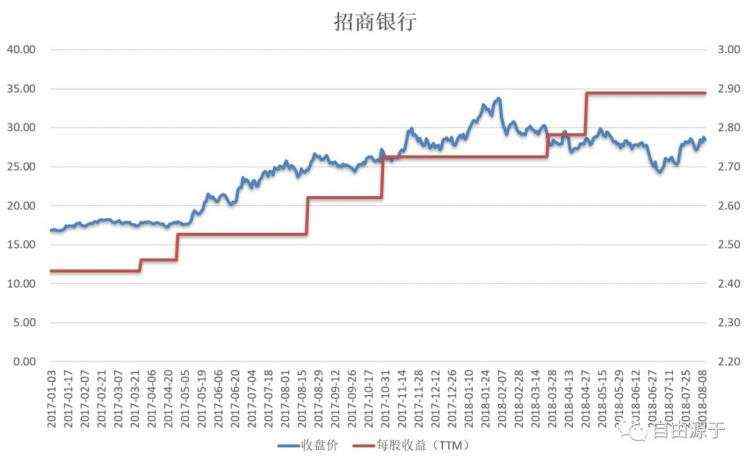
根据季度更新的财务数据和每日更新的价格数据计算每日市盈率

时间序列能做什么

有了时间序列，除了能够进行常用的指标计算（比如20日均价，市盈率等）之外，最重要的用处在于发现序列自身以及序列之间的关系。一旦这种关系确立起来，我们就能够预测序列的未来值。

相关关系

对于序列分析来说，最重要的是看看它们之间是否存在相关关系。

如何来衡量两个序列之间是否相关呢？

一个很自然的想法，是系列可以看作高维的向量，因而可以基于向量与向量之间的夹角来作为距离的定义。夹角越小，距离越小，则两个向量的关联度就越大。

向量夹角的计算，就需要用到余弦公式：

我们将向量之间的内积与模长定义带入到余弦公式，就可以得到序列的相关系数的定义：

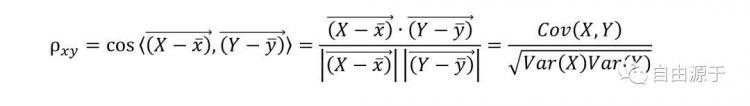
其中，序列X和Y都进行了单位化的操作，通过减去均值去掉相对于原点的偏移，除以方差去掉各自的长度。

有了相关系数，我们就能够定量的衡量序列的关联程度了。

• 相关系数为1，意味着两个序列同向平行，高度正相关（如影随形）；




• 相关系数为-1，意味着两个序列反向平行，高度负相关（南辕北辙）；




• 相关系数为0，则表示两个序列相互垂直，完全不相关（鸡同鸭讲）。

自相关

我们把相关关系作用于序列自身，能够得到序列的过去和序列的现在之间的关系，这个时候得到的相关系数称之为自相关系数。

例如，一个弱平稳序列{rt}的间隔为l的自相关系数为：

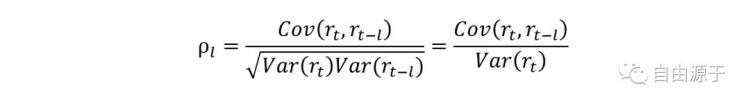
通过自相关分析，我们可以统计出一个价格序列是否是自相关的。比如前文给出的上证指数的收盘价格序列就是自相关的，这一点和我们的直觉相吻合。通常，我们通过指数的收盘价格的均价可以大致推算出下一个交易日的价格范围。然而，上证指数的涨跌幅序列是没有显著的相关性的，也就是说我们不能通过过去几日的涨跌幅推算出下一个交易日的涨跌幅。

由于上证指数的收盘价格序列是自相关的，我们可以通过构造一个自回归模型，来预测未来的价格走势。其基本模型如下：

通过历史数据，可以拟合出模型的参数。在此基础上，就可以对未来价格进行预测啦。

互相关

我们把相关关系作用到两个或者多个不同的时间序列上来，就可以得到序列之间的互相关系数。

在资本资产定价模型中，我们可以通过股票的收盘价格序列与指数的收盘点数序列进行相关分析，从而得到它们之间的贝塔系数。这个数值很有用，可以通过它直观的得到股票价格涨跌与大盘指数涨跌之间的关联强度，并可以在对冲操作中用于计算风险敞口。

招商银行相对于沪深300指数的贝塔系数

总结

时间序列是金融数据的最主要表示方式，如果想从数据中挖掘出有价值的规律或者信息，就需要好好理解并牢牢掌握它。