作者:加勒比海盗530 | 来源:互联网 | 2023-07-14 11:20
近几天对神经网络分类器的学习中,看到了Sigmoid函数。
Sigmoid函数的表达式为:

在Matlab或者Octave中可以画出函数曲线。
t = -60:0.1:60;
S = 1./(1+e.^(-0.2*t));
plot(t,S)
xlabel('x')
ylabel('S(x)')
title('Sigmoid')

可是今天我学到了电机上电,电机有一个加速度,让速度达到一个值。而这个加速度,最好是缓慢增加的,而后要缓慢递减了。这样电机转动会更加平稳。业界喜欢称这个过程是“加减速”。见下图。我们需要把电机转动至目标的速度,速度或者加速度的突变,都有可能引起电流浪涌。因为转子速度突然变化,带电的定子线圈上,会引起反电动势。而加速度的突然变化,由于惯性作用,可能造成机械损伤。因此,对速度和加速度的变化、或者注入电机上的电流和电压,最好都有一个渐进的过程。

(这图片感谢《硬石电机控制专题指导手册_20180515》这部分开源的)
根据理解,最好是让速度和时间的曲线为S形曲线。但是这个曲线在单片机上较难实现。传统的减少速度
加速度突变的方法是用左边的梯形加减速方法。
但是我手头的板子是STM32F4,是一款带有FPU的内核为Cortex-m4的微控制器,所以实时性是有保证的。该MCU的工作频率可达168MHz,我选择每1ms执行一次本算法。这从CPU消耗来看,应该还是十分充裕的。
想起了之前的神经元激活函数Sigmoid,于是上网搜了S形函数,找到了Logistic函数。

经过化简,可得:

这个函数,有三个变量,第一个是K,K是终值;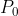 是初值,即当t=0时,曲线对纵坐标横截点。而
是初值,即当t=0时,曲线对纵坐标横截点。而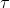 是时间常数。
是时间常数。
下图中,P0不变(P0=0.5),\tau不变(\tau = 1),K变化。蓝色线是K=1,红色线是K=10,绿色线是K=100。

P0=0.5;
K=1;
r=1;t = -10:0.1:10;
Pt = K./(1+(K/P0-1).*e.^(-r*t));
plot(t,Pt,'b')K=10;
Pt = K./(1+(K/P0-1).*e.^(-r*t));
hold on
plot(t,Pt,'r')K=100;
Pt = K./(1+(K/P0-1).*e.^(-r*t));
hold on
plot(t,Pt,'g')
xlabel('t')
ylabel('P(x)')
title('Logistic curve of P0=0.5. t=1. K=1,10,100')
可以见到,曲线最后逼近极限值就是K。
而后,我们改变P0;令时间常数为1,K=10,起始值P0分别为1(蓝色线)、5(红色线)、9(绿色线)。
在Matlab或者Octave执行以下代码:
P0=1;
K=10;
r=1;t = -10:0.1:10;
Pt = K./(1+(K/P0-1).*e.^(-r*t));
plot(t,Pt,'b')P0=5;
Pt = K./(1+(K/P0-1).*e.^(-r*t));
hold on
plot(t,Pt,'r')P0=9;
Pt = K./(1+(K/P0-1).*e.^(-r*t));
hold on
plot(t,Pt,'g')
xlabel('t')
ylabel('P(x)')
title('Logistic curve of P0=1, 5, 9. t=1. K=10')
可显示波形:

初始值,就是t=0时候,P(t)的值。t=0时,P(0)=P0。曲线整体似乎是根据P(0)左右移动。
第三个参数是时间常数。令K=1,P(0)=0.5,\tau 分别是 0.1、1、10

下午试着调这三个参数到平缓,并令函数的输出转换为电机的脉冲速度(电机是步进电机,每一个发送一个脉冲即转动一个角度)。增加每秒内脉冲的个数,即可增加电机的转速。
另外,在减速中,也可以使用本方法,只需要把曲线经过纵轴镜像,即可得到减速的速度曲线。
镜像后的曲线函数:


本文比较思路比较乱……就当作草稿来看吧……国庆节在自己的房间里呆着干活也不容易。
总之,主要讲的是S形曲线。没想到在电机控制这里又用得到。