离散信号半周期傅里叶算法matlab,连续时间信号频谱分析研究及MATLAB实现_离散傅里叶变化论文网...

论文摘要&＃xff1a;信号的频谱分析是信号与系统分析的基础。本文分析了用数值计算的方法实现确知连续时间信号的频谱分析&＃xff0c;即采用离散傅里叶变换的快速算法实现对连续信号的频谱估计&＃xff0c;然后在MATLAB语言工具下结合正弦信号给出了频谱分析的结果。

论文关键词&＃xff1a;频谱分析,离散傅里叶变化

引言

在信号处理过程中&＃xff0c;频域分析方法往往比时域分析方法更方便和有效。对于确知连续时间信号&＃xff0c;其频域分析可以通过连续时间傅里叶变换来进行&＃xff0c;但是&＃xff0c;这样计算出来的结果仍然是连续函数&＃xff0c;计算机不能直接加以处理。为了实现数值计算&＃xff0c;还需要对其进行离散化处理&＃xff0c;即采用离散傅里叶变换(DFT)进行分析。DFT的快速算法的出现&＃xff0c;使DFT在数字通信、图像处理、功率谱估计、系统分析与仿真、雷达信号处理、光学、医学等各个领域都得到广泛应用。本文以正弦信号为例&＃xff0c;介绍用DFT的快速算法即快速傅里叶变化(FFT)实现确知连续时间信号的频谱分析&＃xff0c;给出了MATLAB语言工具下的分析程序。

1信号频谱分析的原理

对于时间连续信号

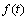&＃xff0c;其频谱分析可以通过连续时间傅里叶变换(CTFT)来进行。连续时间傅里叶变化特别适合于对时间连续信号的理论分析&＃xff0c;但是&＃xff0c;由于函数

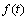和其频谱函数都是连续函数&＃xff0c;不能够直接用计算机来处理&＃xff0c;因此在进行数值计算时必须将其离散化&＃xff0c;然后利用离散傅里叶变换(DFT)实现近似计算。

设对连续时间信号

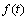的截取时间段长度为

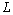&＃xff0c;对其进行离散化的采样时间间隔为

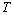,那么采样输出的离散时间序列

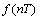中的信号样值点数

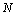为&＃xff1a;

。

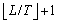例如&＃xff0c;若信号

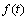的大部分能量集中于频率段

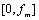和时间段

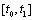上&＃xff0c;那么就可以根据采样定理选取采样时间间隔为

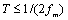&＃xff0c;并选取截取时间段长度为

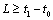。这样就在离散时间点序列

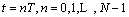上对连续时间信号进行了离散化。对

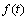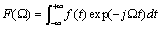
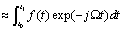
的连续时间傅里叶变化中的积分进行近似求和计算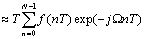&＃xff0c;即&＃xff1a;

(1)

但是&＃xff0c;这样计算出来的结果

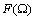仍然是连续函数&＃xff0c;计算机不能直接加以处理。为了实现数值计算&＃xff0c;还需要对

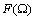进行离散化处理。将频率段

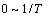Hz划分为

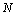个计算频率点&＃xff0c;这

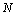个离散频率点以角频率表示为&＃xff1a;

,

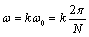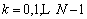(2)

即得到离散频率点上的近似计算式&＃xff1a;

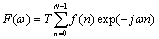(3)

对比DFT计算式&＃xff0c;显然有

(4)

该式表明&＃xff0c;利用DFT(FFT)计算连续时间傅里叶变换的频谱时&＃xff0c;除了计算时域样点的离散傅里叶变化的频谱

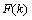&＃xff0c;还要将

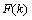乘以取样时间间隔

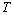&＃xff0c;才能得出结果。

直接计算DFT的复杂度为序列长度的平方&＃xff0c;即

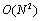。1965年&＃xff0c;库利(T.W.Cooley)和图基(J.W.Tuky)在《计算数学》杂志上发表了著名的《机器计算傅里叶级数的一种算法》论文后&＃xff0c;桑德—图基等快速算法相继出现&＃xff0c;又经人们进行改进&＃xff0c;很快形成了一套高效计算方法&＃xff0c;这就是现在的快速傅里叶算法FFT。其思想是将长序列分解为若干短序列进行DFT计算&＃xff0c;然后通过若干旋转因子的复数乘法和复数加法合成最终的结果。FFT算法中&＃xff0c;如果序列长度是2的幂次&＃xff0c;可将序列长为N的DFT分割为两个长为N/2的子序列的DFT&＃xff0c;成为基2-FFT。快算傅里叶变化算法只需要

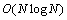的计算复杂度&＃xff0c;FFT算法为数字信号处理技术应用于各种信号的实时处理创造了条件&＃xff0c;大大推动了数字信号处理技术的发展&＃xff0c;在此利用FFT计算连续时间傅里叶变化的频谱。

2频谱分析的若干问题讨论

通过以上原理可知&＃xff0c;连续非周期信号频谱的数值计算必须首先对信号时域采样&＃xff0c;得到时间离散化的信号&＃xff0c;时域采样必须满足或近似满足采样定理。根据时域频域的对应关系&＃xff0c;时域采样将导致所得的抽样信号频谱周期化。然而&＃xff0c;为了使周期化后的抽样信号频谱便于计算机处理&＃xff0c;还必须再将其频域离散化&＃xff0c;方法是对该频谱进行频域采样。根据时域频域的对应关系&＃xff0c;频域离散化将对应于时域信号的周期化。因此&＃xff0c;对于连续非周期信号频谱进行数值计算时&＃xff0c;要确定如何截取信号的时间段、如何选择时域采样率&＃xff0c;以及在时间段上对信号进行截取的方式。截取信号的时间段长度决定了时域周期化的周期&＃xff0c;对应于频率抽样的频率间隔&＃xff0c;即频率分辨率&＃xff1b;时域采样率决定了频域周期化的周期&＃xff0c;即频谱数值计算的范围&＃xff1b;而在某时间段上对信号进行截取的方式&＃xff0c;即不同窗函数的应用&＃xff0c;决定了信号频谱估计的精度和有效范围。

设要分析连续时间非周期信号

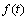在频率范围

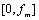内的频谱&＃xff0c;且要求分析的频谱分辨率(数值计算的频率间隔)为

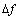&＃xff0c;则首先应根据信号频率范围确定采样率&＃xff0c;在根据所要求的频率分辨率确定截取时间长度&＃xff0c;从而计算出所需计算FFT的序列长度(点数)&＃xff0c;最后根据信号时域波形特性选择使用不同的窗函数。

(1)根据分析的信号频率范围确定采样率。要分析信号在频率范围

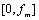内的频谱&＃xff0c;则采样率必须满足采样定理&＃xff0c;即

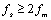&＃xff0c;相应地&＃xff0c;采样时间间隔

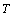(也称为时间分辨率)满足

。

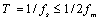(2)根据频率分辨率要求确定分析信号

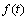的截取时间长度。要使所分析的频率分辨率达到

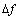&＃xff0c;即每隔

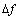计算一个频率点&＃xff0c;那么对信号的截取时间长度

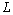必须满足

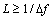&＃xff0c;根据截取时间长度

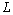和采样时间间隔

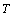就可以计算出截取时间信号离散化之后的序列点数

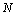&＃xff0c;也可以由计算采样率

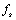和频率间隔

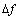来等价计算出序列点数&＃xff0c;即&＃xff1a;

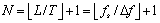(5)

(3)根据信号时域波形特性来应用不同的窗函数。