离散时间信号序列

1、概念

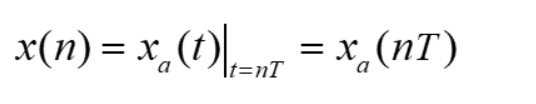
在 n 的定义域内一组有序的数&＃xff0c;也称为序列。n 为整数

2、序列的三种表示方法

2.1、函数表示法

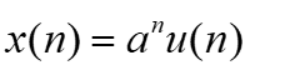
2.2、数列的表示法

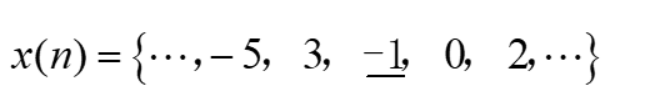
2.3、图形表示法

3、序列的运算

序列的运算都是通过三个基本运算单元 —加法器、乘法器和延时单元实现的。

3.1、基于幅度的运算

当S&＃61;B<无穷时&＃xff0c;称序列x(n)为绝对可和序列&＃xff0c;序列的绝对可和性对于判断序列的傅里叶变换是否存在及判断系统是否稳定具有极重要意义。

3.2、基于对变量(n)的运算

3.2.1、位移

3.2.2、翻褶

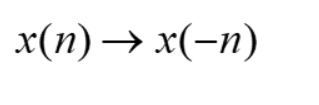
上图表示为&＃xff1a;序列 x(n) 以n&＃61;0 的纵轴为对称轴翻褶得到 x(-n) 。
举个小例子&＃xff0c;如下图所示&＃xff1a;

3.2.3、时间尺度变换

示意如下:
抽样和插值是多抽样率数字信号处理的基础。

3.3、既对幅度运算又对变量(n)运算

3.3.1、差分运算

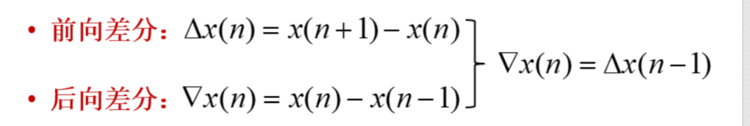示意图如下&＃xff1a;

3.3.2、卷积和运算

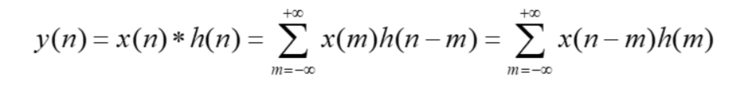关于卷积和的计算&＃xff0c;我将在这个博客中仔细讲解&＃xff1a;https://blog.csdn.net/shouwangyunkai666/article/details/102454968

3.3.3、相关运算

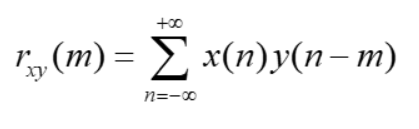
3.3.4、复序列的共轭对称分量和共轭反对称分量