目录
一、时间序列概念与分解模型
1-时间序列数据与基本概念
2-时间序列分解
二、SPSS中七种指数平滑模型
1-七种指数平滑模型简介
2-七种指数平滑模型具体分析
三、ARIMA模型相关的知识点
四、时间序列模型经典案例
1-时间序列建模思路介绍
2-案例1销售数据预测
3-案例2人口数量的预测
4-案例3上证指数的预测
5-GDP增速预测
时间序列也称为动态序列,是指将某种现象的指标数值按照时间顺序排列而成的数值序列。时间序列分析大致可以分成三部分,分别是描述过去,分析规律和预测未来,本次讲将主要介绍时间序列分析中常用的三种模型:季节分解、指数平滑方法和ARIMA模型,并将结合SPSS软件对时间序列数据进行建模。
一、时间序列概念与分解模型
1-时间序列数据与基本概念
正常的数据类型分为三种,分别为横截面数据,时间序列数据,面板数据三类,今天我们主要分析时间序列数据,即同一对象再不同时间连续观察所取得的数据。

时间序列数据包含两个要素,分别为时间要素和数值要素,时间序列可以根据时间和数值性质的不同,可以分为十七时间数据和时点时间数据。

对时期时间数据和时点时间数据如何区分呢,就是时期内的发展结果和时间点上的瞬间水平,一般来说时期的时间序列相加有意义,而时点时间序列相加往往没有实际意义。

2-时间序列分解
时间序列的数值变化规律一般有如下四种,往往是四种变化形式的叠加,这些变化规律就是时间序列分析的切入点。
长期趋势(Secular trend,T)指的是统计指标在相当长的一段时间内,受到长期趋势影响因素的影响,表现出持续上升或持续下降的趋势,通常用字母T表示。
季节趋势(Seasonal Variation,S)是指由于季节的转变使得指标数值发生周期性变动。这里的季节是广义的,一般以月、季、周为时间单位,不能以年作单位。例如雪糕和棉衣的销量都会随着季节气温的变化而周期变化;每年的长假(五一、十一、春节)都会引起出行人数的大量增加。一般用字母S表示。
循环变动(Cyclical Variation,C)与季节变动的周期不同,循环变动通常以若干年为周期,在曲线图上表现为波浪式的周期变动。这种周期变动的特征表现为增加和减少交替出现,但是并不具严格规则的周期性连续变动。最典型的周期案例就是市场经济的商业周期和的整个国家的经济周期。一般用字母C表示。
不规则变动(Irregular Variation,I)是由某些随机因素导致的数值变化,这些因素的作用是不可预知和没有规律性的,可以视为由于众多偶然因素对时间序列造成的影响(在回归中又被称为扰动项)。一般用字母I表示。
以上四种变动就是时间序列变化的分绩结果,可能是一种或者种的组合,四种变动可能是叠加,也可能是乘积。
至于是叠加模型还是乘积模型,根据四种变动之间的关系,独立,则叠加,相互影响,则乘积,需要注意的是一般数据要具有年内周期性,才考虑使用时间序列分解,如果是年份数据则不可以,另外一般序列的季节波动性较大,可以认为各种变动之间关系发生变化,考虑使用 乘积模型,反之,若序列的季节波动性恒定,则考虑使用叠加模型。

我们使用SPSS处理时间序列数据时候,如果有数据确实,可以SPSS自动填充,一般有5中种填充方式,具体如下:
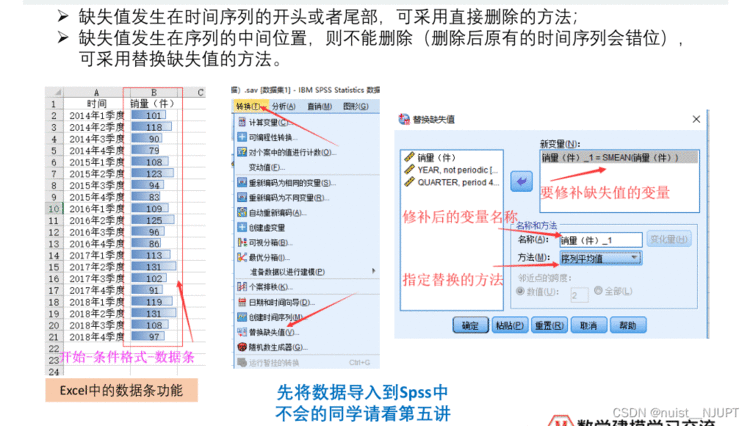
 在SPSS中我们可以定义时间变量,通过定义时间变量,方便后面的时间序列分析,下面看一下定义时间变量的方法。
在SPSS中我们可以定义时间变量,通过定义时间变量,方便后面的时间序列分析,下面看一下定义时间变量的方法。
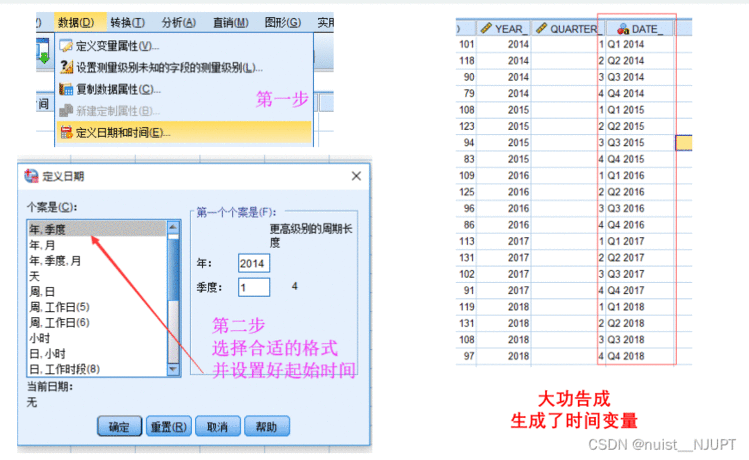
定义好时间变量,我们需要绘制时间序列图并进行时间序列分析,具体如下所示,通过时间序列图,我们可以发现第二季度明显高于其它季度,表现出很强的季节性,但是销售数据的季节波动不大,故可以考虑使用加法分解模型。
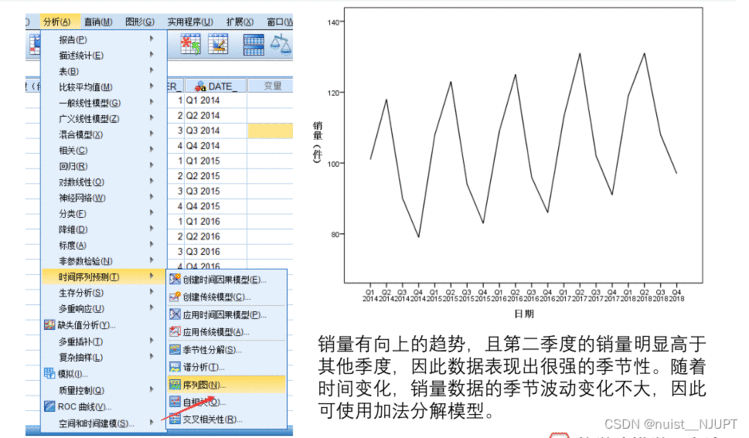 接下来我们使用SPSS进行季节性分解,使用加法模型,具体的操作步骤如下:
接下来我们使用SPSS进行季节性分解,使用加法模型,具体的操作步骤如下:
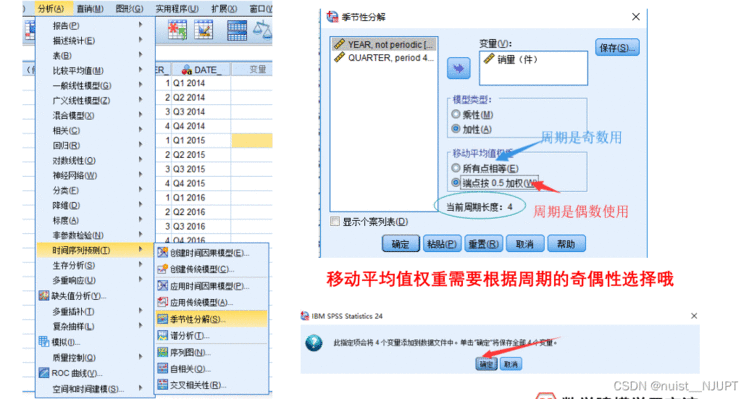
对销售数据进行加法分解得到了季节因子,可以发现第二个季度的季节因子最高,第二季度的平均销量要高于全年平均水平20.93件,第四季度的平均销量要低于全年平均水平19.727件,我们会发现数据中生成了四列,四列分别是残差I,T+C+I,S,T+C四个。
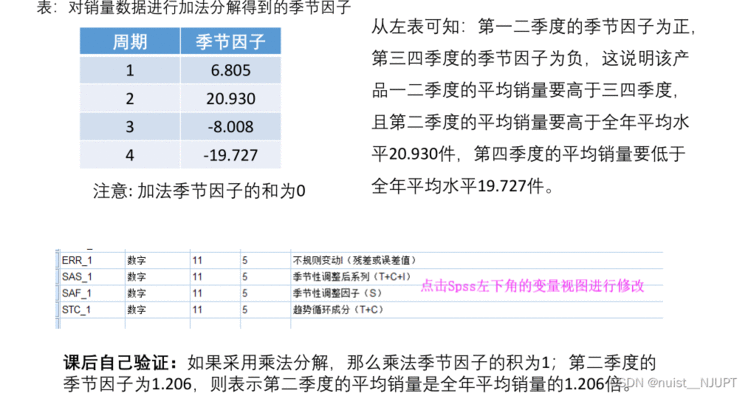 下面我们就可以画出分解后的时序图了,具体如下,使用5个部分作为因变量绘制时序图。
下面我们就可以画出分解后的时序图了,具体如下,使用5个部分作为因变量绘制时序图。
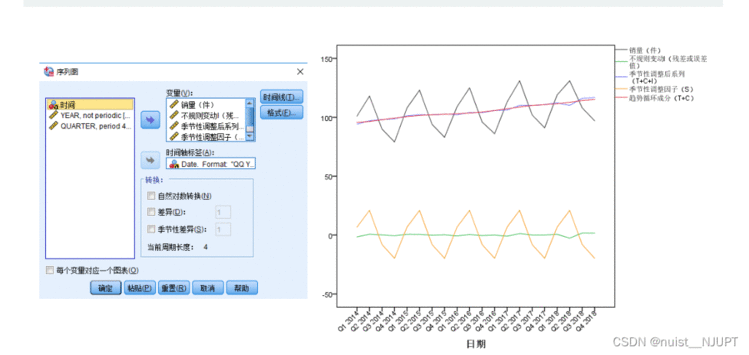
对于时间序列分析,一般的基本步骤入下:作时间序列图,时间序列分解,建立时间序列分析模型,预测未来的指标数值。
二、SPSS中七种指数平滑模型
1-七种指数平滑模型简介
下面我们看一下SPSS中7种指数平滑模型,分别为simple模型,holt线性趋势模型,Brown线性趋势模型,阻尼趋势模型,简单季节模型,winters可加性模型,winters相乘性模型,对于7种指数平滑模型,我们可以简单了解一下它们的适用场景。
simple模型:适用于没有趋势或季节性的序列。
Holt线性趋势模型:适用于具有线性趋势并没有季节性的序列。
Brown线性趋势模型:同上。
阻尼趋势模型:适用于具有线性趋势正在逐渐消失且没有季节性的模型。
简单季节性模型:适用于没有趋势并且季节性影响随时间变动保持恒定的序列。
winters可加性:适用于具有线性趋势和不依赖于序列水平的季节性效应序列。
winters相乘性:适用于具有线性趋势和依赖于序列水平的季节性效应序列。

2-七种指数平滑模型具体分析
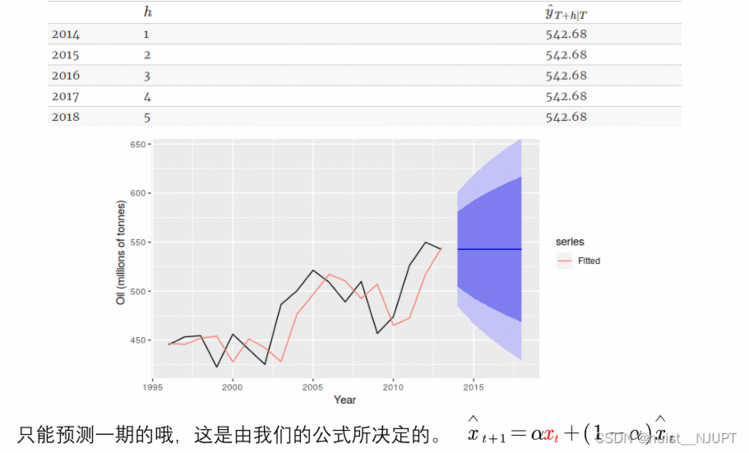
我们先看一下simple模型,即简单指数平滑模型,每一个平滑后的数据都是由过去的数据加权求和所得,越接近当期的数据,权重越大,SPSS的专家建模器会帮我们选择模型,如果选择了simple模型,那么软件会自动帮我们选择一个合适的平滑系数使得误差最小。

不过简单平滑指数预测一般只能预测一期,我们从下面可以发现这是由公式所决定的,由上一期预测当前期。
我们再看一下霍特线性趋势模型,具体如下,适用于含有线性趋势但不含季节成分的,该方法包含一个预测方程和两个平滑方程。每个参数的解释具体如下:

阻尼趋势模型和线性趋势模型很像,也是;两个平滑方程加一个预测方程,只不过再霍特模型的基础之上引入一种阻尼效应,用来缓解较高的线性趋势。通过阻尼参数对模型产生阻尼趋势。

我们再看一下简单季节性模型,需要考虑季节成分,该模型主要由一个水平平滑和一个季节平滑方程,再加上一个预测方程组成 ,其中m是周期的长度,h为超前预期的期数。

我们再看一下,温特加法模型,适用于含有线性趋势和季节成分的模型,包含三个 平滑方程和一个预测方程,一般使用于稳定的季节成分,即随着时间的推移,序列的季节性波动较小,一般可以考虑温特加法模型。

我们看一下最后一个曲线平滑模型,温特乘法模型,和温特加法模型相似,主要区别在于适用于季节成分不稳定的情况,即序列季节性波动较大的情况。

三、ARIMA模型相关的知识点
在介绍ARIMA模型之前,我们需要考虑很多相关的概念,当然只需要了解即可,具体还是放在后面的应用上面,当然了解这些理论有助于理解模型和论文的撰写。

首先我们看一下时间序列的平稳性介绍,一般满足均值和方差固定,协方差只与间隔 S有关,则称该序列xt是白噪声序列,对于严平稳和弱平稳也给出了解释,一般我们考虑弱平稳即可,即协方差平稳。

我们继续看一下差分方程的概念,具体如下所示的方程都可以称为差分方程。

对于差分方程的齐次部分,只包含变量本身和滞后项的式子,具体如下:

下面我们看一下滞后算子,一般用符号L表示,滞后算子由如下三个性质,同时我们可以看到对ARMA模型作差分的具体计算步

我们再看一下AR(p)模型,p阶的自回归模型,就是将自己的1至p阶滞后项视为自变量进行回归,一般该模型适用于受到自身前期因素影响的情况,对于那种受社会因素影响大的情况一般不适用,同时,一般我们考虑的p阶自回归模型,要求时间序列是平稳的。
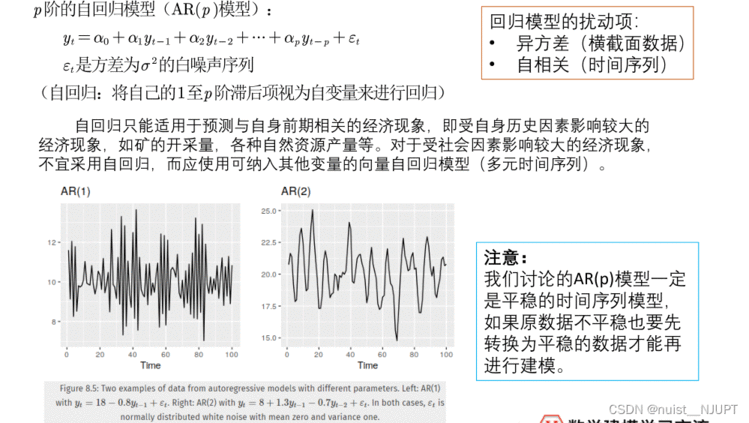
我们继续看一下p阶自回归模型的,我们求出的p个解的模长均小于1,则说明序列平稳。

我们再看一下q阶的移动平均过程,MA(q)模型,
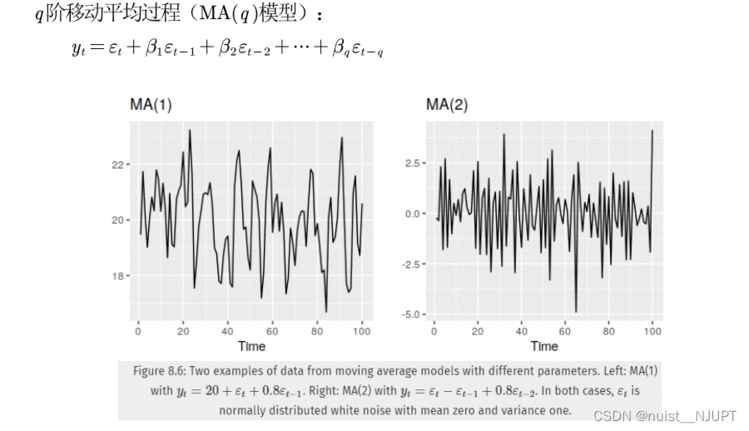
我们具体看一下,为什么有了自回归模型,还需要引入移动平均模型,因为为简化估计参数的工作量,我们尽量使模型中的参数尽可能的少,故考虑引入移动平均模型。

我们继续看一下ARMA模型,其实就是将AR模型和MA模型的组合,共同模拟产生有时间序列样本数据的随机模型过程。
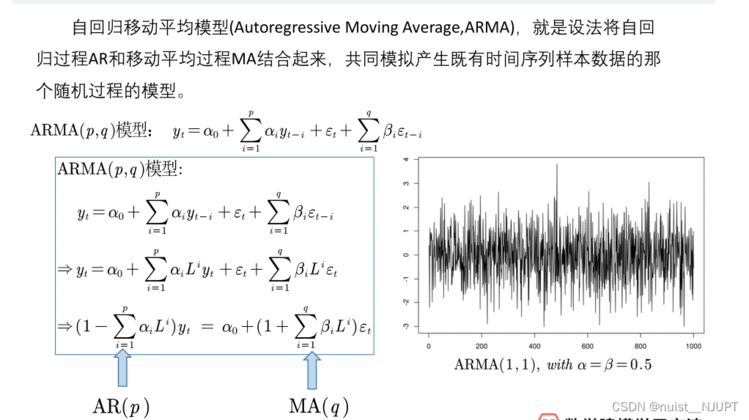
对于ARMA模型,我们也需要考虑平稳性问题, 不过ARMA模型的平稳性只和自回归AR(p)有关。

我们再看一下ARIMA模型,即差分自回归移动平均模型,对于不是平稳的时间序列,我们需要先进行差分处理,转换成平稳时间序列后再建模。

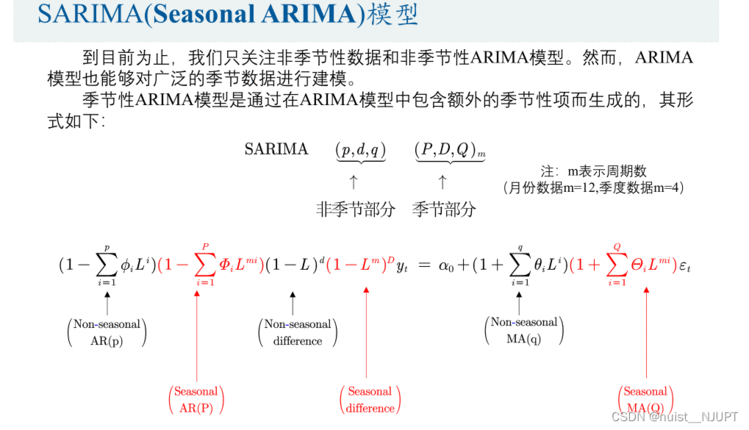
与ARIMA模型相关的还有一个SARIMA模型,就是包含了季节项的ARIMA模型,具体如下所示,非季节部分和ARIMA一致。
四、时间序列模型经典案例
1-时间序列建模思路介绍
正常我们进行时间序列建模,一般按照如下步骤,首先生成时间变量绘制时间序列图,然后考虑是否是季度或者月度数据,有没有明显的季节性波动,判断数据是否是平稳序列,然后就可以使用SPSS的专家建模器帮助我们选择最适合的时间序列模型 ,如果是0阶差分的ARIMA模型,则可以画出样本的ACF和PACF图进行分析,如果得到的是ARIMA(p,1,q)模型,我们则先对数据进行一阶差分,再用ACF和PACF图进行分析,如果得到的结果与季节有关,也可以考虑时间序列分解的方法。

2-案例1销售数据预测
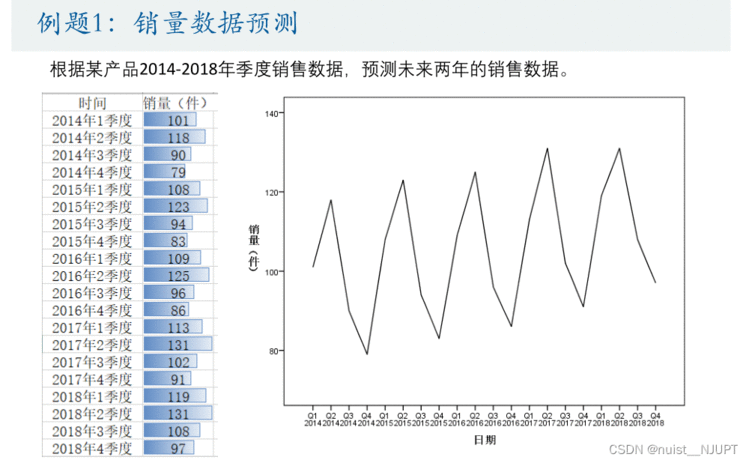
我们看一下给出了4年季度销售数据,预测未来两年的销售数据,我们首先导入数据到SPSS种,然后绘制构造时间变量,绘制时间序列图,如下所示。
通过这个时间序列图,我们可以发现,数据为季度数据,数据不平稳,有上升趋势,我们现在可以使用SPSS的专家建模器,帮助我们选择最合适的时间序列模型。
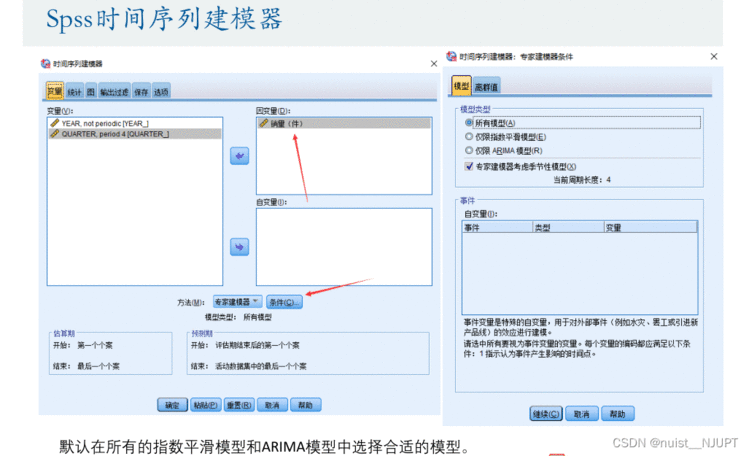
我们点击分析->时间序列预测->创建传统时间序列模型,默认选择最合适的模型,本次系统帮助我们选择的是温特斯加性模型,该模型适用于具有季节性且序列季节变化平稳的情况。
我们需要进行异常值的检测,一般来说,SPSS会自动检测异常值,只需要再离散群种勾选就可以,把下面的异常值检测方法都勾选了,就可以了。

对于统计和图部分,一般勾选如下选项即可,主要用于后面的分析。
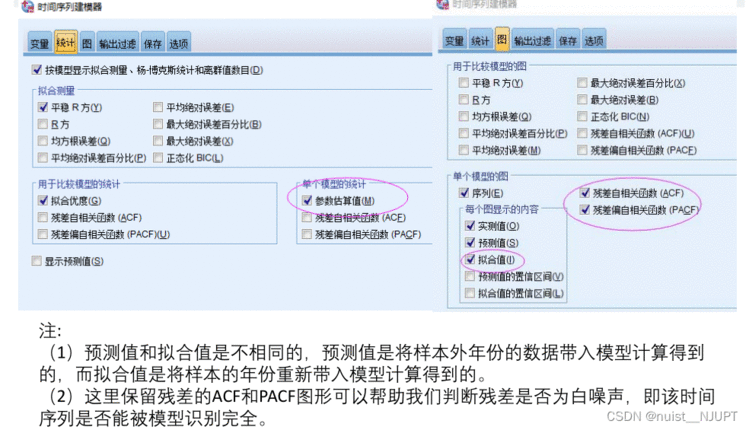
对于剩余几个部分,主要是保存预测值,以及输出预测到第几期,预测到2020年第4个季度,具体操作如下所示。
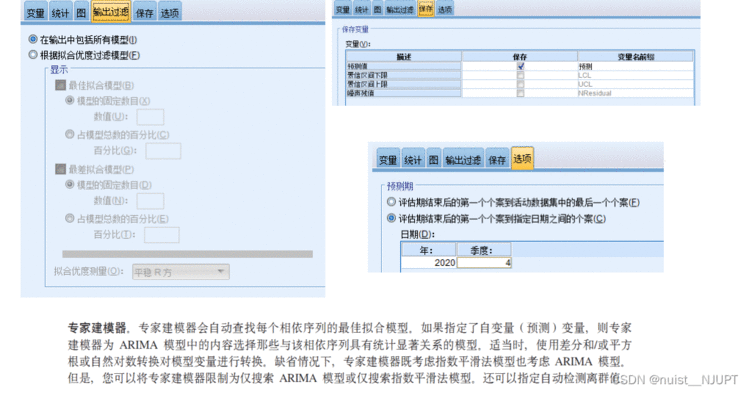
对于时间序列建模在中使用拟合优度测量的定义具体如下,我们会得到一张表,包含如下的参数,根据参数值可以近似判断模型的预测水平。

使用SPSS推荐的温特加法模型,我们可以得到参数估计表,具体如下:

同时,我们可以得到白噪声进行残差检验的结果,滞后项的自相关系数和偏相关系数均与0值没有显著的差异,同时P值大于0.05,我们无法拒绝原假设,则认为残差就是白噪声序列,故模型比较好。
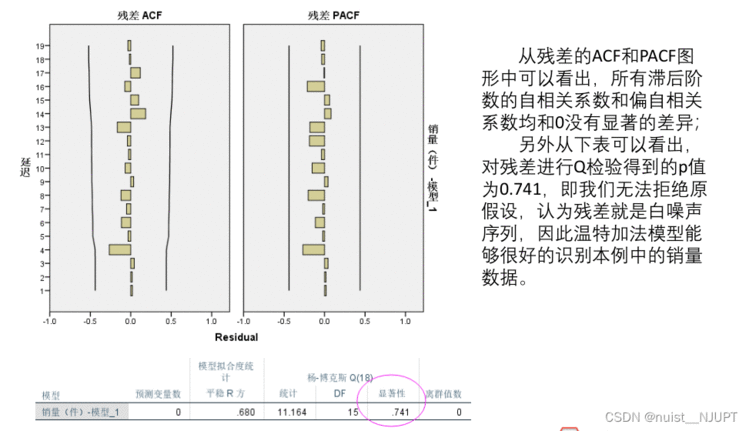 我们看一下预测效果,真实值和拟合值接近,该模型对数据拟合效果较好,该模型能很好的反映销售数据的变化情况。
我们看一下预测效果,真实值和拟合值接近,该模型对数据拟合效果较好,该模型能很好的反映销售数据的变化情况。
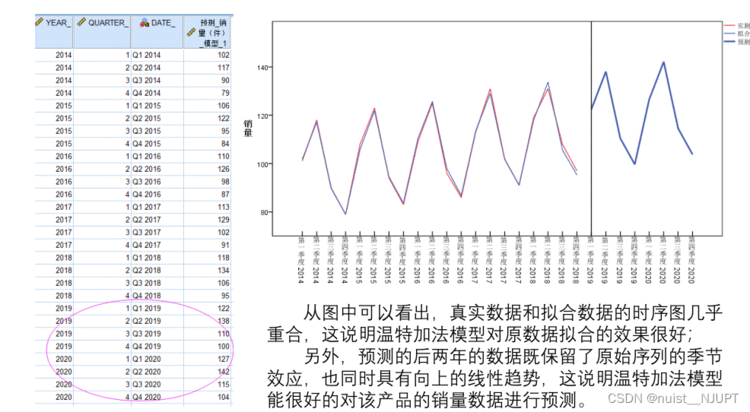
3-案例2人口数量的预测
对于2018年之后年份人口数量的预测,我们首先定义时间变量,然后绘制时间序列图,具体如下所示,基本上是一个线性递增的过程。
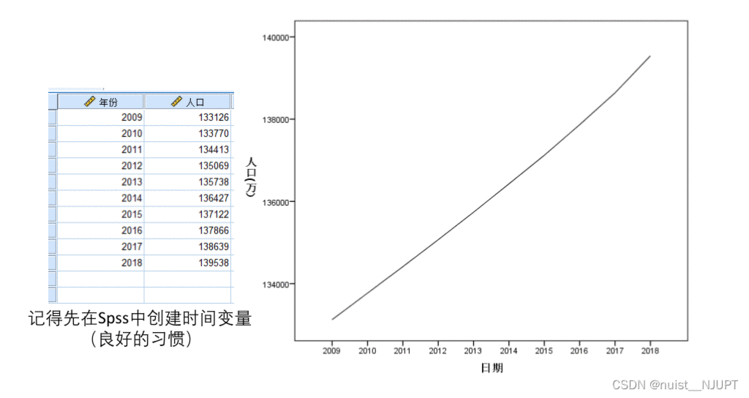
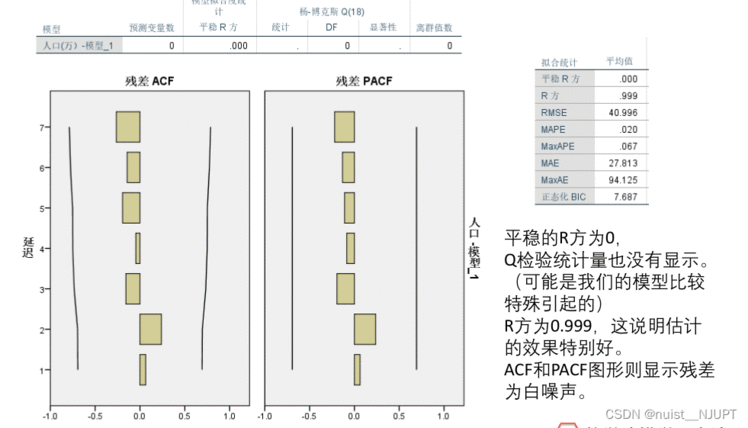
剩余的操作步骤和案例1一样,这边就不再赘述了,我们直接看结果吧,我们可以发现SPSS帮我们选择的是ARIMA(0,2,0)模型, 我们可以得到预测结果如下所示,具体的估算过程如下:

我们看一下残差的白噪声检验,残差为白噪声,模型的预测效果较好。
原始的未来三年人口数量的预测效果图如下所示:
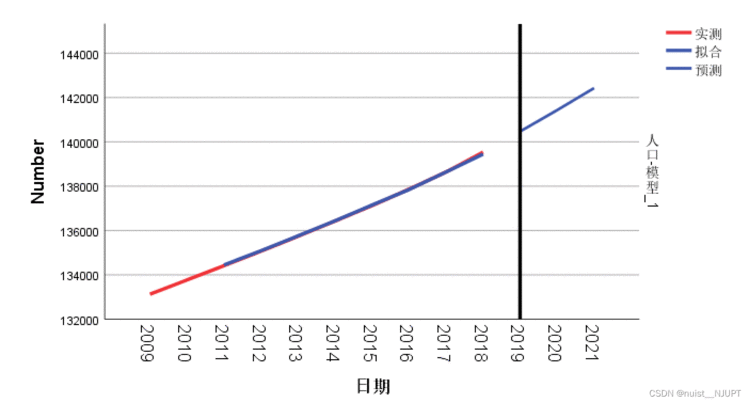
我们可以为其添加标签,这样看起来效果更好,具体的操作步骤如下:
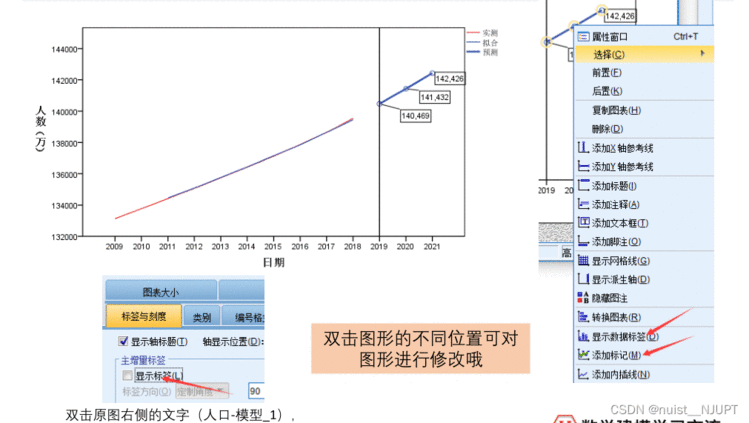
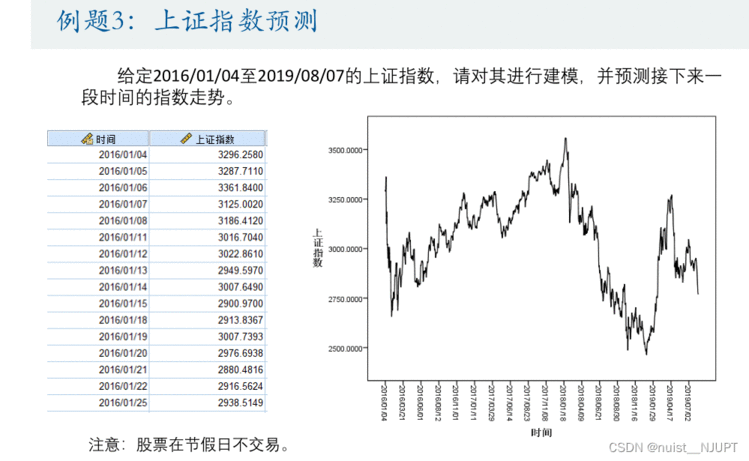
4-案例3上证指数的预测
介绍这个模型主要是想说明前面介绍的时间序列模型对这个数据的预测效果并不好,我们后面会介绍另外的时间序列模型用于预测这一类问题,我们用我们学过的时间序列模型进行预测,观察效果吧,首先需要创建时间变量,绘制时间序列图,具体如下:
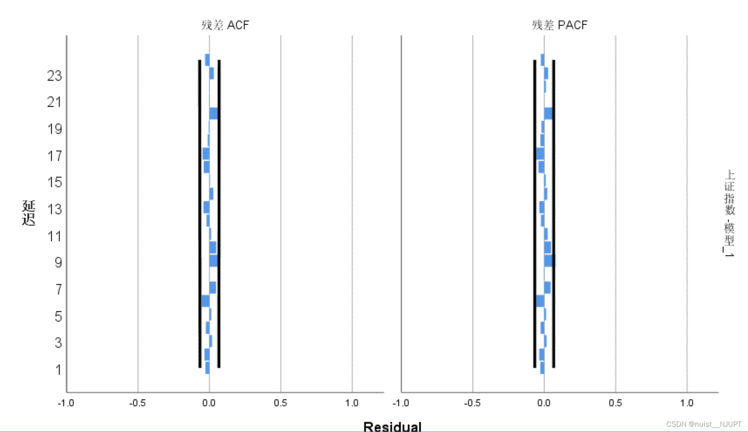
我们看一下使用专家建模器建模的结果,给出的模型是ARIMA(0,1,14),Q值大于0.05,不能拒绝原假设,


另外,ACF和PACF的检验也通过,残差是白噪声。
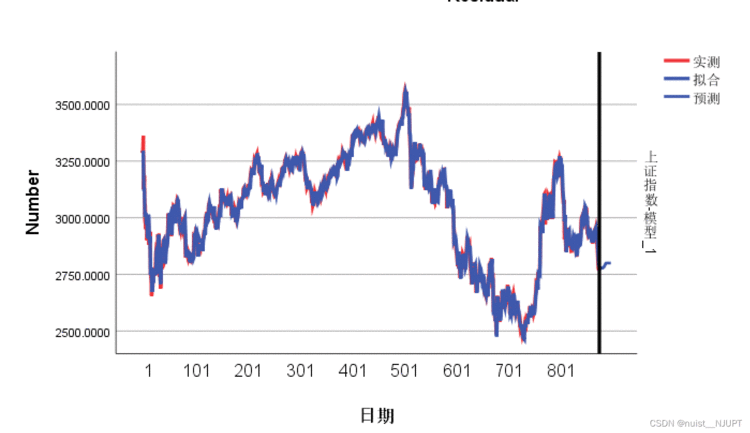
预测效果图如下所示,可以观察到预测的效果较好,该模型能很好的预测。
对于上述模型,我们需要剔除异常值,否则建模效果并不好。
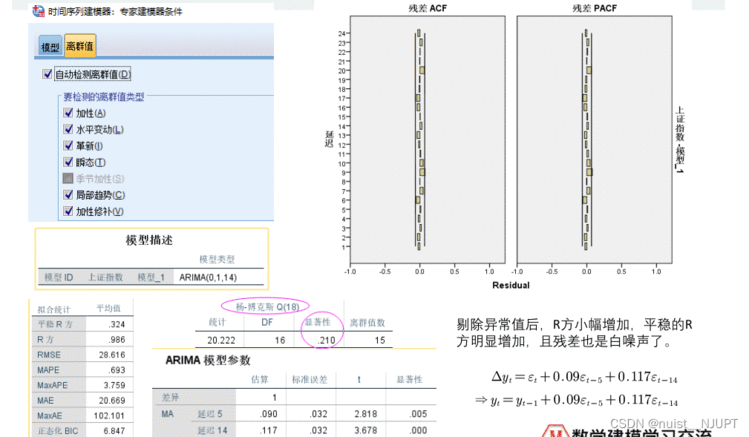
该模可以预测出后14期,超过后14期就不再变化了,具体如下所示。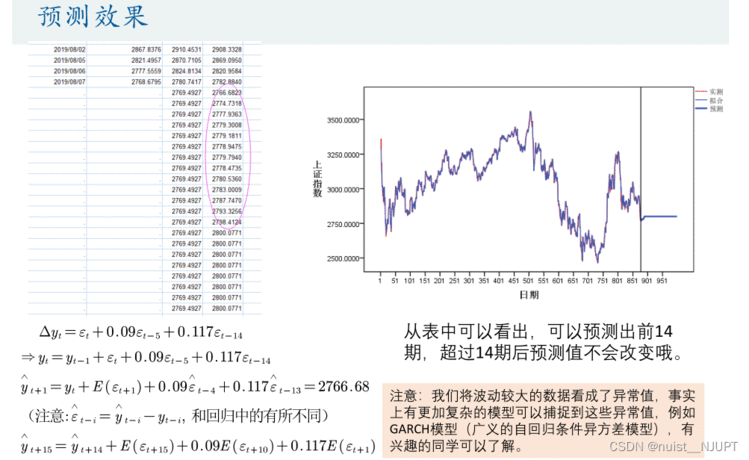
5-GDP增速预测
我们再看一下下面这个例题,通过这个例题,我们主要是学习真正的预测需要结合背景,做出合理假设,而不是直接套模型,下面我们具体看一下吧。
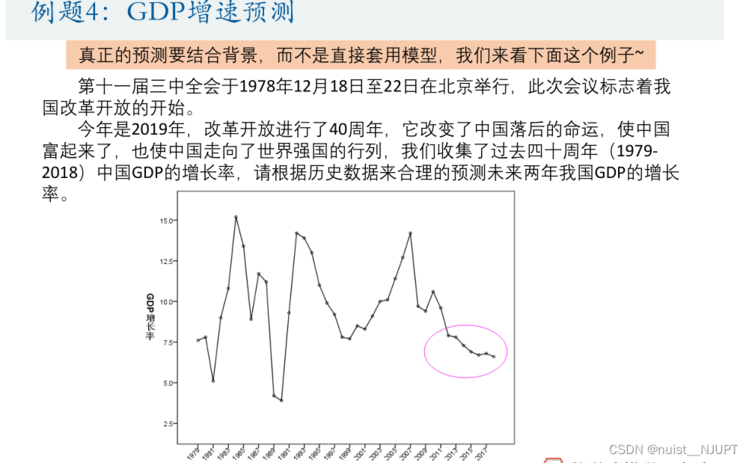 我们使用SPSS建立时间序列模型,预测结果如下:拟合和预测的效果都不是很好,
我们使用SPSS建立时间序列模型,预测结果如下:拟合和预测的效果都不是很好,
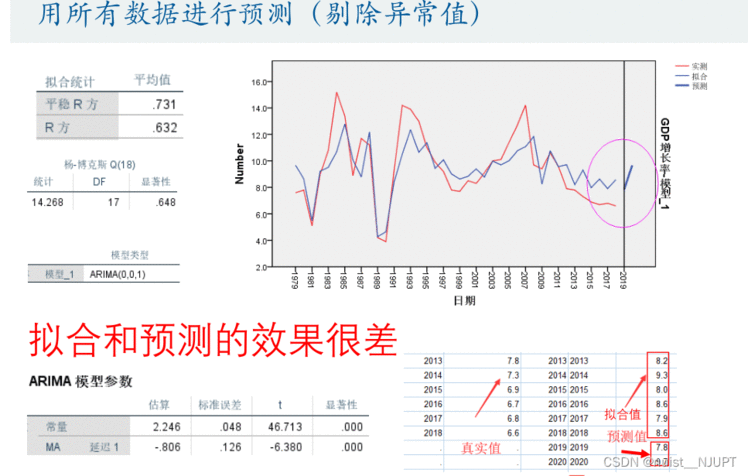
对于可能导致出错的原因,我们认为可能是背景政策的改变,导致的,所以,实际的背景也很重要,要是没有这个因素可能预测效果就比较好。
